Algorithms and Data Structures Glossary

Free glossaries at TanslationDirectory.com

Algorithms and Data Structures Glossary

By www.nist.gov,
Gaithersburg, Maryland, U.S.A.

paul . black [at] nist . gov
http://www.nist.gov/dads

Become a member of TranslationDirectory.com at just $12 per month (paid per year)

Advertisements:

Use the search bar to look for terms in all glossaries, dictionaries, articles and other resources simultaneously

A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z

This is a glossary of algorithms, algorithmic techniques, data structures, archetypal problems, and related definitions. Algorithms include common functions, such as Ackermann's function. Problems include traveling salesman and Byzantine generals. Some entries have links to implementations and more information. Index pages list entries by area and by type. The two-level index has a total download 1/20 as big as this page.

Don't use this glossary to cheat. Teachers, contact us if we can help.

To define or correct terms, please contact Paul E. Black. We need help in automata theory, combinatorics, parallel or randomized algorithms, heuristics, and quantum computing. We do not include algorithms particular to business data processing, communications, operating systems or distributed algorithms, programming languages, AI, graphics, or numerical analysis: it is tough enough covering "general" algorithms and data structures. However, if you want to tackle one of these areas, we'll consider including them.

Some terms with a leading variable, such as n-way, m-dimensional, or p-branching, are under k-. You may find terms dealing with hardware, the computer industry, slang, etc., in the Free On-Line Dictionary Of Computing or in A Glossary of Computer Oriented Abbreviations and Acronyms.

A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z

α: see inverse Ackermann function
ω
Ω
ρ-approximation algorithm
˜
Θ

ω

(definition)

Definition: A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) = ω (g(n)) means g(n) becomes insignificant relative to f(n) as n goes to infinity.

Formal Definition: f(n) = ω (g(n)) means that for any positive constant c, there exists a constant k, such that 0 ≤ cg(n) < f(n) for all n ≥ k. The value of k must not depend on n, but may depend on c.

Note: This is the Greek letter Omega.

Author: PEB

Ω

(definition)

Definition: A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) = Ω (g(n)) means it is more than some constant multiple of g(n).

Formal Definition: f(n) = Ω (g(n)) means there are positive constants c and k, such that 0 ≤ cg(n) ≤ f(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.

Generalization (I am a kind of ...)
big-O notation.

Note: This is the upper-case Greek letter Omega.

This definition is stronger than the traditional mathematical definition. Here, f must be greater than g FOR ALL x bigger than some k. The traditional definition is f is big omega of g if it is not little o of g. That is, one needs only an unbounded sequence of values of x tending to infinity such that cg(x) ≤ f(x) for all x in the sequence.
After Duncan Buell (BUELL@engr.sc.edu) 21 May 2004.

Author: PEB

More information

Donald E. Knuth, Big Omicron and Big Omega and Big Theta, SIGACT News, 8(2):18-24, April-June 1976.

ρ-approximation algorithm

(algorithmic technique)

Definition: An approximation algorithm guaranteed to find a solution at most (or at least, as appropriate) ρ times the optimum. The ratio ρ is the performance ratio or relative performance guarantee of the algorithm.

Generalization (I am a kind of ...)
approximation algorithm.

Note: From Algorithms and Theory of Computation Handbook, pages 32-39 and 34-17, Copyright © 1999 by CRC Press LLC. Appearing in the Dictionary of Computer Science, Engineering and Technology, Copyright © 2000 CRC Press LLC.

Author: CRC-A

˜

(definition)

Definition: (1) Proportional to. (2) Asymptotically equal to. A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) ˜ g(n) means it grows at the same rate as g(n). More formally, it means lim_{x
→ ∞}f(x)/g(x) = 1.

Author: PEB

Θ

(definition)

Definition: A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) = Θ (g(n)) means it is within a constant multiple of g(n). The equation is read, "f of n is theta g of n".

Formal Definition: f(n) = Θ (g(n)) means there are positive constants c₁, c₂, and k, such that 0 ≤ c₁g(n) ≤ f(n) ≤ c₂g(n) for all n ≥ k. The values of c₁, c₂, and k must be fixed for the function f and must not depend on n.

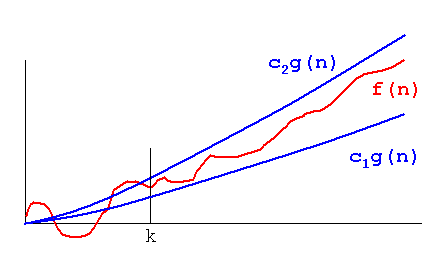
graph showing relation between a function, f, and the limit function, g