Category theory glossary
By
Wikipedia,
the free encyclopedia,
http://en.wikipedia.org/wiki/Glossary_of_category_theory
Become a member of TranslationDirectory.com at just
$12 per month (paid per year)
Advertisements:
Use the search bar to look for terms in all glossaries, dictionaries, articles and other resources simultaneously
This is a glossary of properties and concepts in category theory in mathematics.
Categories
A category A is said to be:
- small provided that the class of all morphisms is a set (i.e., not a proper class); otherwise large.
- locally small provided that the morphisms between every pair of objects A and B form a set.
- Some authors assume a foundation in which the collection of all classes forms a "conglomerate", in which case a quasicategory is a category whose objects and morphisms merely form a conglomerate[1]. (NB other authors use the term "quasicategory" with a different meaning [2].)
- isomorphic to a category B provided that there is an isomorphism between them.
- equivalent to a category B provided that there is an equivalence between them.
- concrete provided that there is a faithful functor from A to Set; e.g., Vec, Grp and Top.
- discrete provided that each morphism is the identity morphism.
- thin category provided that there is at most one morphism between any pair of objects.
- a subcategory of a category B provided that there is an inclusion functor from A to B.
- a full subcategory of a category B provided that the inclusion functor is full.
- wellpowered provided for each object A there is only a set of pairwise non-isomorphic subobjects.
- complete provided that all small limits exist.
- cartesian closed provided that it has a terminal object and that any two objects have a product and exponential.
- abelian provided that it has a zero object, it has all pullbacks and pushouts, and all monomorphisms and epimorphisms are normal.
- normal provided that every monic is normal. [3]
Morphisms
A morphism f in a category is called:
- an epimorphism
provided that g = h whenever
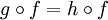 .
In other words, f is the dual of a monomorphism. .
In other words, f is the dual of a monomorphism.
- an identity
provided that f maps an object A to
A and for any morphisms g with domain
A and h with codomain A,
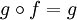 and
and 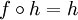 . .
- an inverse
to a morphism g if
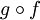 is defined and is equal to the identity morphism
on the domain of f, and
is defined and is equal to the identity morphism
on the domain of f, and 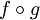 is defined and equal to the identity morphism on
the codomain of g. The inverse of g
is unique and is denoted by g -1
is defined and equal to the identity morphism on
the codomain of g. The inverse of g
is unique and is denoted by g -1
- an isomorphism provided that there exists an inverse of f.
- a monomorphism
(also called monic) provided that g
= h whenever
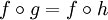 ;
e.g., an injection
in Set.
In other words, f is the dual of an epimorphism. ;
e.g., an injection
in Set.
In other words, f is the dual of an epimorphism.
Functors
A functor F is said to be:
- a constant provided that F maps every object in a category to the same object A and every morphism to the identity on A.
- faithful provided that F is injective when restricted to each hom-set.
- full provided that F is surjective when restricted to each hom-set.
- isomorphism-dense (sometimes called essentially surjective) provided that for every B there exists A such that F(A) is isomorphic to B.
- an equivalence provided that F is faithful, full and isomorphism-dense.
- amnestic provided that if k is an isomorphism and F(k) is an identity, then k is an identity.
- reflect identities provided that if F(k) is an identity then k is an identity as well.
- reflect isomorphisms provided that if F(k) is an isomorphism then k is an isomorphism as well.
Objects
An object A in a category is said to be:
- isomorphic to an object B provided that there is an isomorphism between A and B.
- initial provided that there is exactly one morphism from A to each object B; e.g., empty set in Set.
- terminal provided that there is exactly one morphism from each object B to A; e.g., singletons in Set.
- zero object if it is both initial and terminal, such as a trivial group in Grp.
References
- ^ Adámek, Jiří; Herrlich, Horst, and Strecker, George E (2004) [1990] (PDF). Abstract and Concrete Categories (The Joy of Cats). New York: Wiley & Sons. p. 40. ISBN 0-471-60922-6. http://katmat.math.uni-bremen.de/acc/.
- ^ Joyal, A. (2002). "Quasi-categories and Kan complexes". Journal of Pure and Applied Algebra 175: 207–222.
- ^ http://planetmath.org/encyclopedia/NormalCategory.html
Published - March 2009
This
glossary is available under the terms
of the GNU Free Documentation
Find free glossaries at TranslationDirectory.com
Find free dictionaries at TranslationDirectory.com
Subscribe to free TranslationDirectory.com newsletter
Need more translation jobs from translation agencies? Click here!
Translation agencies are welcome to register here - Free!
Freelance translators are welcome to register here - Free!
Submit your glossary or dictionary for publishing at TranslationDirectory.com
|