Game Theory Glossary
By Wikipedia,
the free encyclopedia,
http://en.wikipedia.org/wiki/Glossary_of_game_theory
Become a member of TranslationDirectory.com at just
$12 per month (paid per year)
Advertisements:
Use the search bar to look for terms in all glossaries, dictionaries, articles and other resources simultaneously
Game theory is the branch of mathematics in which games are studied:
that is, models describing human behaviour. This is a glossary of some
terms of the subject.
Definitions of a game
Notational conventions
Real numbers
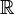
The set of players
N
Strategy space
 ,
where ,
where
Player i's strategy space
 is
the space of all possible ways in which player i can play the game. is
the space of all possible ways in which player i can play the game.
A strategy for player i
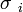 is
an element of is
an element of
complements
 an
element of an
element of  ,
is a tuple of strategies for all players other than i. ,
is a tuple of strategies for all players other than i.
Outcome space
 is
in most textbooks identical to - is
in most textbooks identical to -
Payoffs
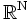 ,
describing how much gain (money, pleasure, etc.) the players are allocated
by the end of the game. ,
describing how much gain (money, pleasure, etc.) the players are allocated
by the end of the game.
Normal form game
A game in normal form is a function:

Given the tuple of strategies chosen by the players, one is
given an allocation of payments (given as real numbers).
A further generalization can be achieved by splitting the game
into a composition of two functions:

the outcome function of the game (some authors call
this function "the game form"), and:

the allocation of payoffs (or preferences)
to players, for each outcome of the game.
Extensive form game
This is given by a tree, where at each vertex of the tree a different
player has the choice of choosing an edge. The outcome set of an extensive
form game is usually the set of tree leaves.
Cooperative game
A game in which players are allowed form coalitions (and to enforce coalitionary
discipline). A cooperative game is given by stating a value for every
coalition:

It is always assumed that the empty coalition gains nil. Solution concepts
for cooperative games usually assume that the players are forming the
grand coalition N, whose value ν(N) is then divided among the players
to give an allocation.
Simple game
A Simple game is a simplified form of a cooperative game, where the possible
gain is assumed to be either '0' or '1'. A simple game is couple (N,
W), where W is the list of "winning"
coalitions, capable of gaining the loot ('1'), and N
is the set of players.
Glossary
Acceptable game
is a game form such that for every possible preference
profiles, the game has pure nash equilibria,
all of which are pareto efficient.
Allocation of goods
is a function  .
The allocation is a cardinal approach for determining
the good (e.g. money) the players are granted under the different outcomes
of the game. .
The allocation is a cardinal approach for determining
the good (e.g. money) the players are granted under the different outcomes
of the game.
Best reply
the best reply to a given complement  is a strategy
is a strategy  that
maximizes player i's payment. Formally, we want: that
maximizes player i's payment. Formally, we want:
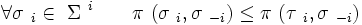
Coalition
is any subset of the set of players:
Condorcet winner
Given a preference ν on the outcome space,
an outcome a is a condorcet winner if all non-dummy
players prefer a to all other outcomes.
Dictator
A player is a strong dictator if he can guarantee any outcome regardless
of the other players  is
a weak dictator if he can guarantee any outcome, but his strategies
for doing so might depend on the complement strategy vector. Naturally,
every strong dictator is a weak dictator. Formally: is
a weak dictator if he can guarantee any outcome, but his strategies
for doing so might depend on the complement strategy vector. Naturally,
every strong dictator is a weak dictator. Formally:
m is a Strong dictator if:

m is a Weak dictator if:
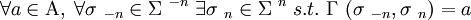
Another way to put it is:
a weak dictator is α-effective for every possible outcome.
A strong dictator is β-effective for every possible outcome.
A game can have no more than one strong dictator. Some games have multiple
weak dictators (in rock-paper-scissors both players are weak dictators
but none is a strong dictator).
See Effectiveness. Antonym: dummy.
Dominated outcome
Given a preference ν on the outcome space,
we say that an outcome a is dominated by outcome b
(hence, b is the dominant strategy) if it
is preferred by all players. If, in addition, some player strictly prefers
b over a, then we say that a
is strictly dominated. Formally:
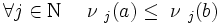 for
domination, and for
domination, and
 for
strict domination. for
strict domination.
An outcome a is (strictly) dominated
if it is (strictly) dominated by some other outcome.
An outcome a is dominated for a coalition
S if all players in S prefer some
other outcome to a. See also Condorcet winner.
Dominated strategy
we say that strategy is (strongly) dominated by strategy  if
for any complement strategies tuple if
for any complement strategies tuple  player
i benefits by playing player
i benefits by playing .
Formally speaking: .
Formally speaking:
 and and
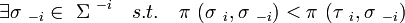
A strategy σ is (strictly) dominated if it is
(strictly) dominated by some other strategy.
Dummy
A player i is a dummy if he has no effect on the
outcome of the game. I.e. if the outcome of the game is insensitive
to player i's strategy.
Antonyms: say, veto, dictator.
Effectiveness
A coalition (or a single player) S is effective for
a if it can force a to be the outcome
of the game. S is α-effective if the members of
S have strategies s.t. no matter what the complement
of S does, the outcome will be a.
S is β-effective if for any strategies of the
complement of S, the members of S
can answer with strategies that ensure outcome a.
Finite game
is a game with finitely many players, each of which has a finite set
of strategies.
Grand coalition
refers to the coalition containing all players. In cooperative games
it is often assumed that the grand coalition forms and the purpose of
the game is to find stable imputations.
Mixed strategy
for player i is a probability distribution P on  It
is understood that player i chooses a strategy randomly
according to P. It
is understood that player i chooses a strategy randomly
according to P.
Mixed Nash Equilibrium
Same as Pure Nash Equilibrium, defined on the space
of mixed strategies. Every finite game has Mixed
Nash Equilibria.
Pareto efficiency
An outcome a of game form π
is (strongly) pareto efficient if it is undominated
under all preference profiles.
Preference profile
is a function  This
is the ordinal approach at describing the outcome of
the game. The preference describes how 'pleased' the players are with
the possible outcomes of the game. See allocation of goods. This
is the ordinal approach at describing the outcome of
the game. The preference describes how 'pleased' the players are with
the possible outcomes of the game. See allocation of goods.
Pure Nash Equilibrium
An element  of
the strategy space of a game is a pure nash equilibrium point if no
player i can benefit by deviating from his strategy of
the strategy space of a game is a pure nash equilibrium point if no
player i can benefit by deviating from his strategy 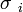 given
that the other players are playing in given
that the other players are playing in 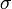 Formally: Formally:

No equilibrium point is dominated.
Say
A player i has a Say if he is not a Dummy,
i.e. if there is some tuple of complement strategies s.t. π (σ_i)
is not a constant function.
Antonym: Dummy.
Value
A value of a game is a rationally expected outcome.
There are more than a few definitions of value, describing
different methods of obtaining a solution to the game.
Veto
A veto denotes the ability (or right) of some player to prevent a
specific alternative from being the outcome of the game. A player who
has that ability is called a veto player.
Antonym: Dummy.
Weakly acceptable game
is a game that has pure nash equilibria some of which
are pareto efficient.
Zero sum game
is a game in which the allocation is constant over different outcomes.
Formally:

w.l.g. we can assume that constant to be zero. In a zero sum game,
one player's gain is another player's loss. Most classical board games
(e.g. chess, checkers) are zero sum.
Published - February 2011
Text is available under the Creative
Commons Attribution-ShareAlike License; additional terms may apply.
See Terms
of Use for details.
Find free glossaries at TranslationDirectory.com
Find free dictionaries at TranslationDirectory.com
Subscribe to free TranslationDirectory.com newsletter
Need more translation jobs from translation agencies? Click here!
Translation agencies are welcome to register here - Free!
Freelance translators are welcome to register here - Free!
Submit your glossary or dictionary for publishing at TranslationDirectory.com
|


